For a side-project of mine I’m looking at Kademlia (Wikipedia), which is used in peer-to-peer (P2P) systems. One problem of P2P systems is that nodes come and go randomly. So it’s not easy to retrieve stored data. Where to store data? And then how to find it again? What happens if a node with the data disappears?
 A group of algorithms for this problem exists under the name of Distributed Hash Tables (DHT). These algorithms create a shared identity for the data and the nodes of the P2P system. Most of the time a hash function creates the shared identity. The hash function is applied to the data as well as to the node identities. To store a given piece of data, the algorithm chooses the node with the most similar identity.
A group of algorithms for this problem exists under the name of Distributed Hash Tables (DHT). These algorithms create a shared identity for the data and the nodes of the P2P system. Most of the time a hash function creates the shared identity. The hash function is applied to the data as well as to the node identities. To store a given piece of data, the algorithm chooses the node with the most similar identity.
Different algorithms exist, for example Koord, Chord, Pastry, Tapestry, to achieve the shared identity and to decide where to store the data. Kademlia uses a so-called XOR metric. This metric allows a fast, stable, unique comparison of the data and the node identities. It expresses distance between two nodes. Kademlia uses this to choose which nodes it connects to. In such a way, even if there are many nodes, it is possible to find the closest nodes to a given piece of data.
Implementations
There exist many implementations for Kademlia, but for my project they were not usable. Some of them are not generic enough and couldn’t use the node identities from my project. Others were very old, or directly linked with the network code. And some projects simply didn’t implement all of Kademlia. So I did what every good programmer does: implement my own.
One confusing part of the paper is the discussion of the XOR metric and the corresponding figures which show the node identities without the XOR metric. Another confusing part is an optimization for some corner cases. Only with the help of the Wikipedia entry did I understand the description.
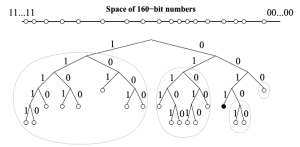
So I thought about the problem in terms of the XOR metric, and I think it’s easier, and hopefully correct. The XOR metric calculates the distance of two nodes as the result of XORing their identities together. Then the result is interpreted as a number describing the distance. The algorithm creates a view of the network which concentrates on close nodes and stores fewer far away nodes. One of the main problems is how to create this view of the network.
The node lists
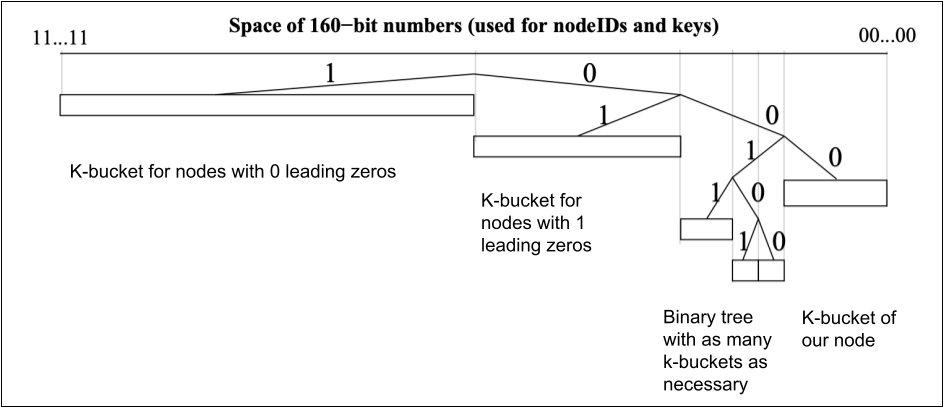
A k-bucket is a list of nodes with k or fewer entries. If a new node arrives but the corresponding bucket is already full, the system puts the node in a waiting list. The Kademlia protocol also describes how to update the node list, and how to find a faraway node. Here I’m just describing how to handle the k-buckets:
- The tree stores k-buckets of nodes for the most distant nodes to the left. Every number of leading zeros gets its own bucket, starting with 0.
- Our node is to the right, as any ID XOR itself equals to 0. Our node is also in a k-bucket, but the closest nodes form a binary tree of k-buckets, for the purpose of keeping as many close nodes as available.
- If the k-bucket with our node inside grows too big, the following happens: the k-bucket is split into two, and the binary tree is reduced to a new k-bucket with one more leading zero.
Routing data
The original Kademlia protocol describes that if a node wants to find a given piece of data, the node needs to discover itself the closest node to this data. However, this will make many connections. And as my system uses WebRTC, I would like to try a multi-hop routing system, where requests for data travel through the network until they find the requested data.